坐标变换(2D)

教程3DWebGL

变换（Transforms）和仿射变换（Affine Transforms）

在计算机图形学中，变换（Transforms）是一种用于改变对象位置、方向、大小或形状的操作。它们是将对象从一个坐标空间变换到另一个坐标空间的数学操作。而仿射变换（Affine transformations）是一种特殊类型的变换，它保持了原始对象的直线性质和平行性质。仿射变换是一种线性变换，意味着它保持了原始对象的直线性质和平行性质。在仿射变换中，原始对象的平行线在变换后仍然是平行的。在计算机图形学中，仿射变换通常用于实现基本的图形操作，如对象的平移、旋转和缩放。它们也常用于构建更复杂的变换操作，如透视投影等。

仿射变换（Affine transformations） 是一种线性变换，它包括以下几种基本变换：

1. 平移（Translation）：沿着坐标轴移动对象的位置。
2. 旋转（Rotation）：围绕一个点或轴线旋转对象。
3. 缩放（Scaling）：增加或减少对象的大小。
4. 剪切（Shearing）：按比例移动对象的顶点，从而改变其形状。

这些变换可以单独应用，也可以组合在一起以实现更复杂的效果。

在二维空间中，仿射变换通常由一个 2x2 的矩阵和一个平移向量（通常表示为一个 2x1 的列向量）组成，表示为：

在三维空间中，仿射变换通常由一个 3x3 的矩阵和一个平移向量（表示为一个 3x1 的列向量）组成，表示为：

平移(Translation)

平移公式推导

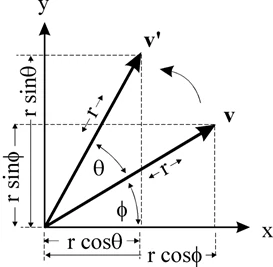
旋转(Rotation)

绕Z轴旋转公式推导

---

缩放(Scale)

缩放公式推导

二维矩阵

平移

平移矩阵推导

注意

代码中存储矩阵数据时，为了方便存储和获取矩阵的某一列，所以代码的实现和数学中矩阵的惯例是不一样的：

• 矩阵的数学表达：

  const some4x4TranslationMatrix_math = [
        1,  0,  0,  tx, // row 1
        0,  1,  0,  ty, // row 2
        0,  0,  1,  tx, // row 3
        0,  0,  0,  1,  // row 4
  ];

• 矩阵的代码实现：

  const some4x4TranslationMatrix_webgl = [
        1,  0,  0,  0,  // row 1 = column 1 of math convention 
        0,  1,  0,  0,  // row 2 = column 2 of math convention 
        0,  0,  1,  0,  // row 3 = column 3 of math convention 
        tx, ty, tz,  1, // row 4 = column 4 of math convention 
  ];

使用矩阵实现平移：

旋转

旋转矩阵推导

使用矩阵实现平移、旋转：

缩放

缩放矩阵推导

投影

#version 300 es
in vec2 a_position; // 顶点的原始坐标（本地坐标、模型空间坐标）
uniform float u_heightWidthRatio; // canvas.clientWidth / canvas.clientHeight

void main() {
    gl_Position = vec4(a_position, 0.0, 1.0); // gl_Position: clipping space 中的坐标
    gl_Position.x *= u_heightWidthRatio; // 修正为 NDC
}

观察上面修正 NDC 的方法，发现其实就是对 Y 轴进行的缩放变换（即投影变换），故此我们可以把这一步骤加到平移、旋转、缩放等仿射变换中。

投影矩阵推导

另一种坐标系

前面的例子中，采用的坐标系是以屏幕中心为原点、Y轴朝上为正数，一般在 2D 中是采用另一种坐标系：

• 屏幕左上角为原点
• Y轴朝下为正数

●————————————————————————> X轴
| 原点(0,0,0) 
|
|
|
|
|
v Y轴

采用 2D 常用坐标系：