矩阵(Matrix)

教程图形学

本节讲解计算机图形学中有关矩阵的知识点。

矩阵(Matrix)的定义

矩阵是由行列数字排列构成的二维矩形阵列，表达如下：

Missing or unrecognized delimiter for \left\mathbf{M}=\left\[\begin{array}{cccc} M\_{00} & M\_{01} & \cdots & M\_{0,(n-1)} \\ M\_{10} & M\_{11} & \cdots & M\_{1,(n-1)} \\ \vdots & \vdots & \ddots & \vdots \\ M\_{(m-1), 0} & M\_{(m-1), 1} & \cdots & M\_{(m-1),(n-1)} \end{array}\right]

我们称之为矩阵，英文读作 "m by n"。

我们用大写粗体字母表示一个矩阵，例如
用大写细体加下标的形式表示矩阵中的一个元素(entry)，例如表示第行第列的元素
也被叫做第项

WARNING

由于编程中的数组下标是从 0 开始的，所以我们也从 0 开始标记矩阵元素。

EXAMPLE

上面是一个 (2行3列)的矩阵，

其中第1行第1列元素，

第2行第3列元素。

方阵

当即行数与列数相同的矩阵称为方块矩阵，间称方阵

单位矩阵

主对角线元素全是 1，其他元素全是 0 的方阵，称为单位矩阵(identity matrix)，我们用来表示：

TIP

Missing or unrecognized delimiter for \left\begin{aligned} \mathbf{I}\_n &=\left\[\begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{array}\right] \\ \mathbf{A}*{m \times n} \mathbf{I}*{n} &= \mathbf{A}\_{m \times n} \\ \mathbf{I}*{n} \mathbf{B}*{n \times p} &= \mathbf{B}\_{n \times p} \\ \end{aligned}

行列式

一个方阵的行列式记作或，是通过以下公式计算得出的标量。

行列式公式

是 $次对称群$ (symmetric group)，共有个排列组合；
是中的某个排列组合，是排列中的第个元素；
是 the sign of
- 如果是偶排列，则；
- 如果是奇排列，则；
是求和符号，是连乘符号。

请参考行列式公式视频讲解 :::

行列式的运算律

运算律	公式
单位方阵的行列式
矩阵转置的行列式
矩阵逆的行列式
行列式的乘法规则
行列式的标量分解

行列式的意义和应用

一个矩阵的行列式可以被认为是这个矩阵的有方向的大小(magnitude)。

1阶行列式

的矩阵(也就是一个数)，其行列式也就是这个数：

注意：这里的符号不是绝对值符号。 :::

2阶行列式

的矩阵，其行列式是该矩阵的 2 个列向量形成的平行四边形的有向面积。

点 积 公 式 三 角 函 数

3阶行列式

的矩阵，其行列式是该矩阵的 3 个列向量形成的平行六面体的有向体积。

混 合 积

请继续参考叉积的应用-计算体积

对角线

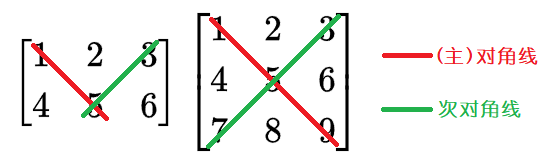
从最左上角的元素至最右下角的元素的连线称为对角线或主对角线(main diagonal 或 principal diagonal)，其上的元素称为主对角线元素，

不在主对角线上的元素称为非对角线元素(off-diagonal entries)。

相似的，从最右上角的元素至最左下角的元素的连线称为次对角线(minor diagonal)或反对角线(antidiagonal)，其上的元素称为次对角线元素。

TIP

在矩阵中，

一个元素：

如果满足则其为主对角线元素，
如果满足则其为次对角线元素。

注意：下标是从 0 开始的 :::

对角矩阵(diagonal matrix)

所有非对角线元素为零的矩阵称为对角矩阵。

EXAMPLE

上三角矩阵(superdiagonal matrix)

对角线左下方的元数全部为零的矩阵称为上三角矩阵。

EXAMPLE

下三角矩阵(subdiagonal matrix)

对角线右上方的元数全部为零的矩阵称为下三角矩阵。

EXAMPLE

转置矩阵

矩阵的转置用表示：

的行等于的列；
的列等于的行；

对于矩阵，其转置为：

转置公式

INFO

矩阵的转置可以被想象成是该矩阵沿着对角线的反射。

对称矩阵

如果，那么该矩阵称为对称矩阵(symmetric matrix)。

EXAMPLE

INFO

对称矩阵肯定是方阵
对角矩阵肯定是对称矩阵

反(斜)对称矩阵

如果，那么该矩阵称为反对称矩阵(antisymmetric matrix)或斜对称矩阵(skew-symmetric matrix)。

EXAMPLE

列向量和行向量

维向量可以被看作为或的矩阵，分别叫做列向量(column vector)和行向量(row vector)。

EXAMPLE

向 量 形 式 矩 阵 列 向 量 形 式 矩 阵 行 向 量 形 式

WARNING

在数学文献中，传统的做法是将一个向量写成一个单列的矩阵，所以我们也遵循这个规则，即采用列向量形式。

矩阵可以被看作是列(行)向量的数组：

这种表示方法将在我们要讨论的矩阵变换 TODO中很有意义。 :::

TODO 列主序和行主序存储

矩阵运算

按位的加法、减法，与标量的乘法、除法

假设都是的矩阵，，那么：

公式

EXAMPLE

矩阵乘法

假设有矩阵和矩阵，前者的列数与后者的行数相同，则两者可以相乘，乘积为一个矩阵。

乘法公式

即乘积的第项是的第行与的第列的点积。

EXAMPLE

第0行第0列

第0行第1列

第1行第0列

第1行第1列

运算律

运算律	公式
结合律
分配律
分配律
标量因式分解
标量乘法交换律
转置乘积规则

三阶矩阵乘法

公式展开

矩阵与列向量相乘

公式展开

Missing or unrecognized delimiter for \left\begin{aligned} \mathbf{M} &= \begin{bmatrix} M\_{00} & M\_{01} & M\_{02} \\ M\_{10} & M\_{11} & M\_{12} \\ M\_{20} & M\_{21} & M\_{22} \end{bmatrix} = \begin{bmatrix} \mathbf{a} & \mathbf{b} & \mathbf{c}\ \end{bmatrix} \\ \mathbf{M v} &=\left\[\begin{array}{lll}M\_{00} & M\_{01} & M\_{02} \ M\_{10} & M\_{11} & M\_{12} \ M\_{20} & M\_{21} & M\_{22}\end{array}\right]\left\[\begin{array}{l}v\_x \ v\_y \ v\_z\end{array}\right] \\ &=\left\[\begin{array}{l}M\_{00} v\_x+M\_{01} v\_y+M\_{02} v\_z \ M\_{10} v\_x+M\_{11} v\_y+M\_{12} v\_z \ M\_{20} v\_x+M\_{21} v\_y+M\_{22} v\_z\end{array}\right] \\ &=\fcolorbox{red}{transparent}{$v\_{x}\mathbf{a} + v\_{y}\mathbf{b} + v\_{z}\mathbf{c}$} \end{aligned}

如果，那么；

因此可以发现，的几何意义在于：的 1、2、3 列分别告诉我们 x、y 和 z 轴是如何在通过建立的新坐标系中重定位的。

INFO

以上是坐标变换 TODO的关键概念。

逆矩阵

就像数有倒数一样，矩阵也有相同的概念：

逆矩阵

上述公式中，我们称为的逆矩阵。

请参考逆矩阵的计算方法：

WARNING

逆矩阵存在的条件：

一定是方阵
矩阵的行列式不为 0

运算律	公式
加法结合律
加法交换律
标量乘法结合律
标量乘法交换律
标量乘法分配律
标量乘法分配律

滤镜

矩阵(Matrix)

矩阵(Matrix)的定义

方阵

单位矩阵