向量(Vector)

教程数学

本节讲解计算机图形学中有关向量的知识点。

向量(Vector)的定义

空间中从起点指向终点的有向线段，称为向量。

也可以用小写字母加箭头表示：
或者使用小写粗体正体字母表示：

n 维空间向量的数学描述

其中被称为向量的分量(component)。 :::

3 维空间向量的数学描述

或 或

其中的 3 个分量分别是在 X,Y,Z 轴上的分量。 :::

INFO

向量也叫做矢量。

向量的特性

向量有 2 个重要的特性：

方向(direction)；
长度(size 或 magnitude)，用或或表示。

向量的长度也叫做模。 :::

INFO

一个物体的重量，一条路的长度，这些被称为标量(scalar)；向量(vector) 则是在标量的基础上，加上了方向。

举例说明：

空间中两点之间的有向线段，我们用向量表示，既包含了线段的方向，也包含了两点之间的距离；
一颗发射中的子弹，我们用向量表示，既包含了子弹的方向，也包含了子弹的速度；
施加在一个物体上的力，我们用向量表示，既包含了力的方向，也包含了力的大小。

WARNING

向量没有绝对的起始坐标，如果向量和只是起始点不一样，但是方向和长度一样，则

WARNING

，细体的表示空间中一个点的坐标，不是向量；

，粗体的表示这是一个向量，长度= 1、方向=平行于X轴正方向。

示例说明

点击展开/折叠示例

EXAMPLE

新窗口打开

上面的 3 维演示空间中：

点，点；
向量 = = (1, 3, -2) - (-1, 1, 0) = (2, 2, -2)；
长度。

向量运算

长度

向量的长度计算公式如下：

向量长度计算公式

假设 n=3，即 3 维空间，那么：

EXAMPLE

3 维向量 = (2, 2, -2)，

那么。

零向量(Zero Vector)

所有分量为 0 的向量被称为零向量(Zero Vector)：

零向量

单位向量(Unit Vector)和归一化(Normalization)

如果，那么我们称为单位向量；我们用来表示一个单位向量。

保持一个向量的方向不变、把它的长度变为 1，称为向量归一化，公式如下；

向量归一化公式

EXAMPLE

，那么，

WARNING

长度为 0 的向量无法归一化

与标量的乘法和除法

假设为一个标量，那么：

向量与标量相乘和相除

EXAMPLE

，，那么

，

。

与标量相乘(除)的意义

当时，结果向量的方向不变，长度被扩大(缩小)了倍；
当时，结果向量的方向相反，长度被扩大(缩小)了倍；
当时，相乘的结果向量为零向量，相除则没有意义。

在下面的演示中，左右滑动来观察的变化：

点击展开/折叠示例

新窗口打开

向量和标量相乘(除)满足以下运算律

运算律	公式
结合律
交换律
分配律
分配律

加法和减法

向量之间的加减法是按位操作的

EXAMPLE

，，那么，

，

。

向量加(减)法的意义

的意义在于：形成了一个新的向量
- 把的起点放在的终点
- 新向量的起点为的起点，终点为的终点
，即对取反后相加，意义同加法。

点击展开/折叠示例

下面演示了向量的加法和减法：

新窗口打开

向量的加减法满足以下运算律

运算律	公式
结合律
交换律

按位的乘法和除法

向量间的按位相乘(除)

EXAMPLE

，，那么，

，

。

INFO

向量间按位的乘法和除法没有物理意义，一般用在着色器语言中对颜色值的操作。

点积（Dot Product）

向量点积公式

当 n = 3 时，

EXAMPLE

，，那么，

。

INFO

因为点积的结果是一个标量，所以点积也被称为数量积(scalar product，还可以翻译为标量积)。

点积满足以下运算律

运算律	公式
交换律
分配律
标量因式分解

点积的矩阵表达公式

如果把向量看作列矩阵，那么：

点积的矩阵表达公式

Missing or unrecognized delimiter for \left\mathbf{a} \cdot \mathbf{b}=\mathbf{a}^{\mathrm{T}}\mathbf{b}=\left\[\begin{array}{} a\_{0} & a\_{1} & \cdots & a\_{n-1} \end{array}\right]\left\[\begin{array}{} b\_{0} \\ b\_{1} \\ \vdots \\ b\_{n-1} \end{array}\right]

点积的意义和应用

点积的三角学公式

其中，为向量之间的平面夹角（0° ≤ ≤ 180°）。 :::

点积的意义和应用

可以通过点积了解向量之间的相互关系，例如向量间夹角的大小、是否平行、是否垂直等。

当时，说明；
当时，说明；
当时，说明，即垂直于，此时称和是正交的；
当向量平行时（即），；
求向量间的夹角：因为，所以；
求向量在向量上的投影：
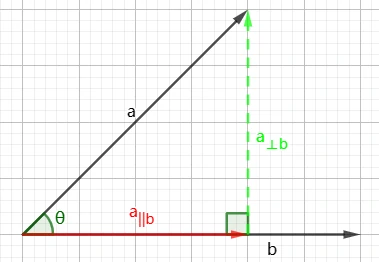
a 在 b 上的投影
以上公式中的是与同方向的单位向量，
$⟂$ 叫做 the rejection of a from b
- $⟂$
- $⟂$ :::

点击展开/折叠示例

在以下的演示中，拖拽 A/B/C 点以改变的大小，观察点积的结果：

新窗口打开

+++

点积三角学公式推导

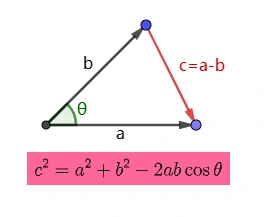
根据上图中的余弦定理，可知：

使用运算律展开公式(2)中红色区域：

对比公式(2)和(5)中的方框区域，可知：

推 导 结 束

叉积（Cross Product）

3 维向量叉积公式

EXAMPLE

，那么，

INFO

因为叉积的结果是一个矢量，所以点积也被称为向量积(vector product，还可以翻译为矢量积)。

WARNING

点积适用于所有维度的向量，但是叉积仅适用于 3 维向量，因为叉积的本质是楔积 TODO。

叉积满足以下运算律

运算律	公式
反交换律
分配律
标量因式分解
拉格朗日公式
拉格朗日公式
拉格朗日恒等式 (Lagrange's identity)

叉积的矩阵表达公式

用列矩阵的形式表达向量 :

用构建一个特殊的反对称矩阵：

然后：

叉积的意义和应用

前置知识

请阅读《3 维空间坐标系》相关内容，了解左/右手坐标系的判断方法和区别。

一般 3D 渲染库都采用右手坐标系，因此以下内容都是基于右手坐标系的。

叉积的三角学公式

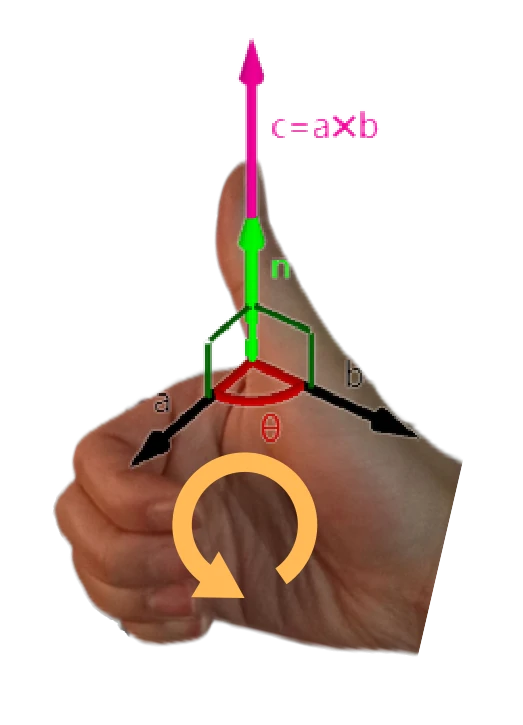
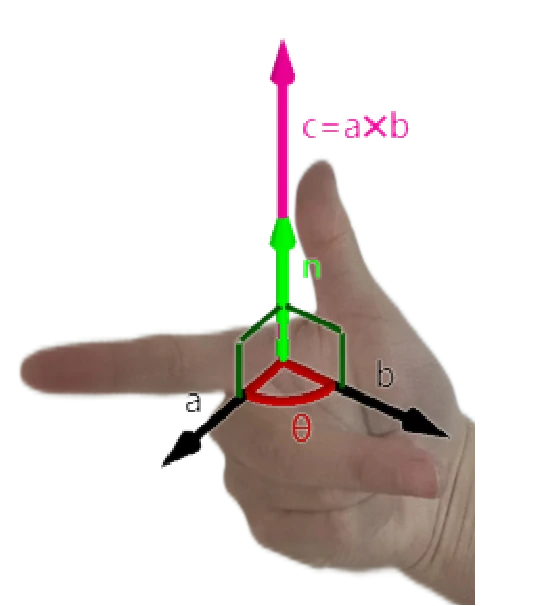
其中，为的夹角，为垂直于的单位向量。 :::

叉积的意义和应用

可以通过叉积计算法线、面积和体积等。

计算顶点的法线
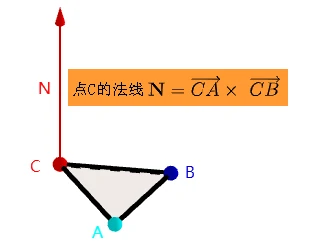
顶点法线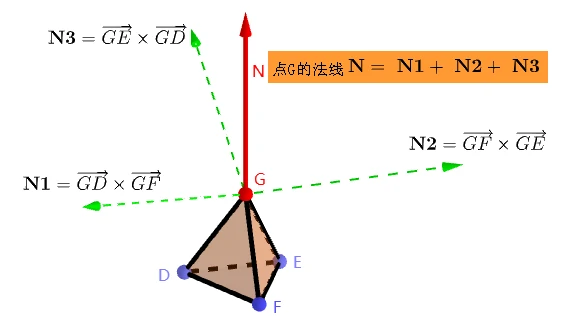
共享顶点法线

计算面积
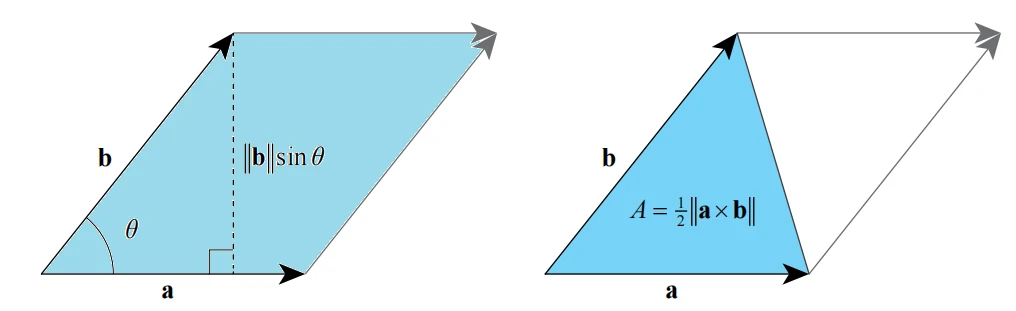
平行四边形和三角形的面积
上图左侧的平行四边形的高度为，因此面积为，正是叉积的模；
右侧的三角形面积是平行四边形面积的，因此。
计算体积
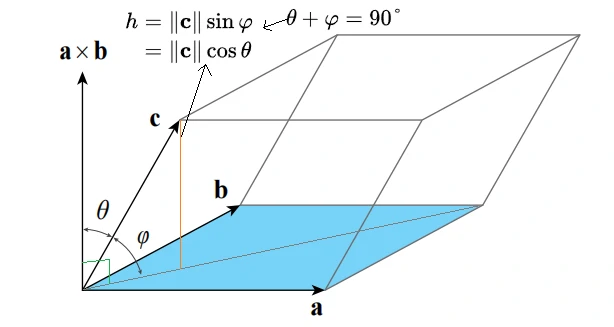
平行六面体的体积
$上图中平行六面体的底面积高所以体积向量混合积$
:::

叉积三角学公式推导

使 用 点 积 公 式 展 开 满 足 三 项 式 乘 法 公 式 满 足 三 项 式 平 方 公 式 使 用 点 积 三 角 学 公 式 展 开 拉 格 朗 日 恒 等 式 求 平 方 根 推 导 结 束

其中红色区域的公式是为了拼凑三项式乘法公式而添加的。 :::

向量投影

两个或多个向量相加组成(compose)一个新的向量，把一个指定的向量分解成两个或多个向量的相加，此过程称为向量分解(decomposing)。

最常见的向量分解是把一个向量分解成与 x、y、z 轴平行的 3 个投影向量，如下所示：

点击展开/折叠示例

EXAMPLE

新窗口打开

+++

TIP

如上所示，给定向量 :

分别是平行于 x、y、z 轴的单位向量；
分别是在或 x、y、z轴上的投影向量；

求向量在任意非零向量上的投影，请参考点积的应用-向量投影，另外：

TIP

Missing or unrecognized delimiter for \left\begin{aligned} \mathbf{a\_{|b}} &= \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^{2}} \mathbf{b} \\ &= \frac{1}{|\mathbf{b}|^{2}} \underbrace{(\mathbf{a} \cdot \mathbf{b}) \mathbf{b}}*{\Downarrow\text{矩阵形式}\Downarrow} \\ &= \frac{1}{|\mathbf{b}|^{2}} \mathbf{b} \mathbf{b}^{\rm T} \mathbf{a} \\ &= \frac{1}{|\mathbf{b}|^{2}} \underbrace{\left\[\begin{array}{ccc} b\_x^2 & b\_x b\_y & b\_x b\_z \\ b\_x b\_y & b\_y^2 & b\_y b\_z \\ b\_x b\_z & b\_y b\_z & b\_z^2 \end{array}\right]}*{\text{外积 outer product}} \left\[\begin{array}{l} a\_x \\ a\_y \\ a\_z \end{array}\right] \end{aligned}

外积公式

我们用来表示向量之间的外积(outer product)：

假 设 那 么

Missing or unrecognized delimiter for \left\mathbf{u} \otimes \mathbf{v}=\mathbf{u v}^{\mathrm{T}}=\left\[\begin{array}{l} u\_x \\ u\_y \\ u\_z \end{array}\right]\left\[\begin{array}{lll} v\_x & v\_y & v\_z \end{array}\right]=\left\[\begin{array}{lll} u\_x v\_x & u\_x v\_y & u\_x v\_z \\ u\_y v\_x & u\_y v\_y & u\_y v\_z \\ u\_z v\_x & u\_z v\_y & u\_z v\_z \end{array}\right]

混合积

向量的混合积(scalar triple product 标量三重积)是指两个向量的叉积结果与第三个向量进行点积，结果是一个标量，公式如下：

混合积公式

关于混合积的应用，请参考叉积的应用-计算体积。

滤镜

向量(Vector)

向量(Vector)的定义

向量的特性

示例说明

向量运算